August 3rd, 2024
What is Cluster Analysis? Definition, Examples, & More
By Connor Martin · 12 min read
In statistical analysis, many methods operate within a supervised framework, relying on assumptions and predefined labels to model relationships and predict outcomes. Cluster analysis isn’t one of these methods.
Cluster analysis operates unsupervised, focusing on uncovering natural groupings and patterns of data without prior categorization. In fact, this method is the one to create categories – aka clusters – based on similarity or distance measures between all the data points.
Thanks to cluster analysis, statistics can also be used to explore a complex dataset and reveal its underlying structure. With this in mind, let’s dig a little deeper into this unique – and highly valuable – statistical method.
Defining Cluster Analysis in Statistics
As previously mentioned, cluster analysis works by organizing data points into groups (clusters) based on how closely they resemble each other. Using cluster analysis algorithms, researchers arrive from Point A – a larger population or a sample – to Point B – a smaller subset of clusters where data points share similarities or characteristics.
Researchers never know how many clusters will emerge beforehand. Instead, the cluster analysis algorithm usually determines the optimal number based on data similarity metrics. Every single one of those clusters should contain extremely homogenous data.
Let us give you an example.
An e-commerce business might use a clustering algorithm to analyze the purchasing behaviors of all their customers. The algorithm might categorize these customers based on characteristics like average spending per transaction, frequency of purchases, and product preferences. The business can then use this classification to tailor its marketing efforts and only target specific clusters with specific offers. For instance, customers who tend to spend the most money might receive exclusive invitations to high-end product launches or VIP events.

Why Is Cluster Analysis Helpful?
With cluster analysis, researchers can derive meaningful insights from complex datasets, even with no prior knowledge of how the data points should be categorized. As such, this method is vital for uncovering hidden patterns, effectively segmenting data, and facilitating further exploration.
How to Conduct a Cluster Analysis
So, a clustering algorithm creates clusters. That much is clear by now. But how does one actually conduct a clustering analysis from beginning to end? Learn the answer to this question in the step-by-step guide below.
Step 1 - Define the Objective
Let’s say a fitness center is trying to optimize its training programs by understanding member preferences and behaviors. This will be the objective for this cluster analysis and generally the first step anyone performing cluster analysis should take.
Step 2 - Prepare the Data
To achieve its goal, the fitness center will look into its visitors’ behavior, including two key variables – “preferred exercise type” (e.g., cardio, strength training, yoga) and “frequency of gym visits.” Why these two clustering variables? Because they’re the most likely to provide actionable insights the fitness center needs to tailor its programs effectively.
Step 3 - Choose the Cluster Analysis Type
This guide will touch on different cluster analysis types a bit further down the road. For now, let’s just say that the fitness center decides to use the K-means algorithm for “frequency of gym visits” (numerical data) and K-medoid clustering for “preferred exercise type” (categorical data).
Step 4 - Run the Algorithm
Step 4 is where the actual cluster analysis takes place. Using the chosen clustering algorithms – K-means and K-medoids – the fitness center identifies clusters representing different member profiles based on their exercise preferences and visit frequency.
Step 5 - Validate the Clusters
Sure, the clustering algorithms take care of the analysis. However, the result of this analysis shouldn’t be taken at face value. No, the clusters must be first validated. Validating a cluster simply means ensuring each group is truly homogenous internally (high intra-cluster similarity) and distinct from other groups (low inter-cluster similarity).
Step 6 - Interpret the Results
After validating the clusters, it’s time to reveal what they truly mean. Each cluster should represent a specific member profile. For instance, there can be a cluster with members who prefer cardio and visit the gym every day and another one with yoga enthusiasts who only attend the gym once a week.
Step 7 - Apply the Findings
Now, we get to the whole point of performing cluster analysis – using the different clusters to inform strategic decisions and actions. In the case of our fitness center, the organization might introduce daily cardio-intensive workout challenges for the high-frequency cardio cluster. Similarly, the yoga cluster might receive specialized yoga workshops and meditation sessions on a weekly basis.
Types of Cluster Analysis
There are thousands of clustering algorithms aiming to find different ways to group data points into clusters. With this in mind, it shouldn’t be surprising there’s also more than one type of cluster analysis (as mentioned above). Here’s a brief overview of the primary ones.
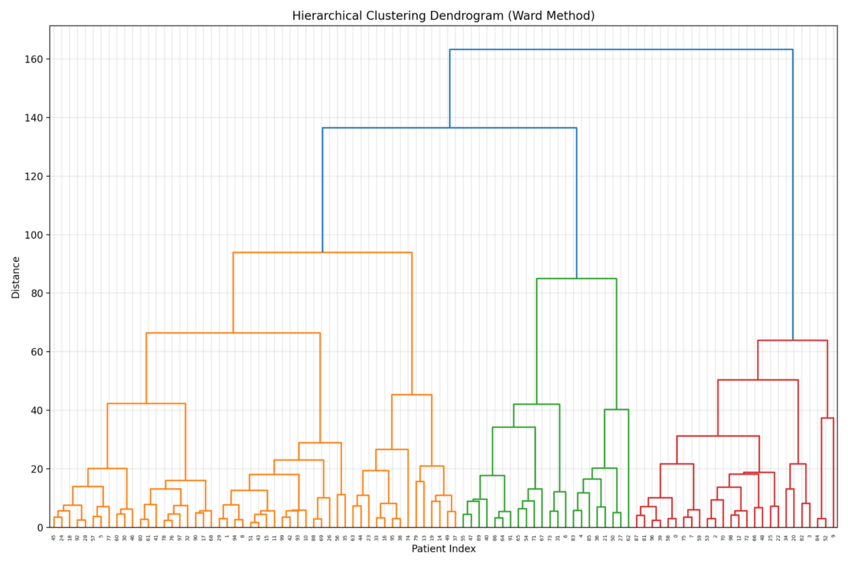
Hierarchical Clustering
The hierarchical cluster analysis has a pretty self-explanatory name. It creates a hierarchy of clusters by repeatedly merging or splitting them based on their similarities. The end goal is for every single data point to belong to the same cluster.
Take files and folders on your hard disc as an example. All your photos will belong to the “Photos” cluster but will be organized into subfolders like “Vacations” and “Portugal 2024” based on similarities like location or date.
K-Means Clustering
K-means clustering groups of data points into a predetermined number of clusters, labeled as “k,” based on their similarity to the centroid of each cluster. The centroid in question is the average value of all the data points in the cluster. For instance, the centroids for a small retail store can be the average purchase amounts of $20, $100, and $500, and all customers spending similar sums would be classified into one of the three clusters.
K-Medoids Clustering
K-medoid clustering is quite similar to K-means clustering. But instead of using mean centroids, this method relies on medoids, aka actual data points from the dataset. This is what makes it more suitable for datasets with non-numeric or categorical attributes.
When to Use Cluster Analysis
Cluster analysis can be used for any project requiring data segmentation or categorization based on similarities of the data points. This includes instances like:
- Market research (market segmentation)
- Resource allocation (in manufacturing, logistics, healthcare, etc.)
Practical Examples of Cluster Analysis
Now that you know the broader uses of cluster analysis, let’s list some concrete examples to help you understand this method better:
- E-commerce: Performing customer segmentation based on demographics, purchasing behavior, and product preferences
- Healthcare: Uncovering whether different geographical areas report higher or lower instances of specific diseases
- Psychology: Classifying patients based on similar behavioral patterns
- Education: Identifying students with special needs based on their behavior, aptitudes, and achievements
- Biology: Clustering species based on their phenotypic characteristics
Simplify Cluster Analysis with Julius AI
If you find cluster analysis highly beneficial but the process of cluster analysis is too confusing or time-consuming, we’ve got just the solution for you. Julius AI. Think of this AI-powered data analysis tool as ChatGPT but for math and data. In other words, all it needs is a prompt from you (the data you’ve gathered), and it can quickly and efficiently perform the cluster analysis you need.
Frequently Asked Questions (FAQs)
What are the four types of cluster analysis?
The four main types of cluster analysis are hierarchical clustering, K-means clustering, K-medoids clustering, and density-based clustering. Each method has its strengths, with hierarchical clustering creating nested clusters, K-means and K-medoids grouping based on centroids or medoids, and density-based clustering identifying clusters of arbitrary shapes based on data density.
What are the basic requirements of cluster analysis?
Cluster analysis requires a clear objective, a well-prepared dataset with relevant features, and a similarity or distance measure to group data points. Additionally, selecting an appropriate clustering algorithm and validating the resulting clusters are crucial for ensuring meaningful and actionable results.
What are the disadvantages of clustering?
Clustering methods can be sensitive to outliers, require careful parameter selection (like the number of clusters), and may struggle with high-dimensional or overlapping datasets. Additionally, interpreting clusters can be subjective, and results may vary depending on the chosen algorithm and similarity measures.
